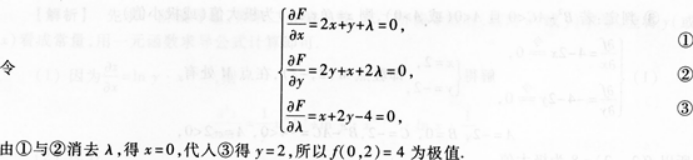【正确答案】:
解设F((x,y,λ)=(x,y)+λ(x+2y-4)=x2+y2+xy+λ(x+2y-4),
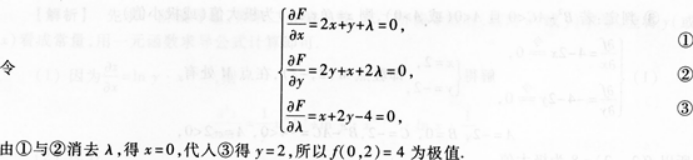
【题目解析】:这是利用拉格朗日乘数法来求条件极值。通过构造拉格朗日函数 F((x,y,λ)=x²+y²+xy+λ(x+2y-4),对其分别求关于 x、y、λ的偏导数,并令偏导数都等于 0,可得到一个方程组,解这个方程组就能求得可能的极值点。然后进一步判断这些点是极大值还是极小值。具体计算过程在给出的图片中详细展示了。
解设F((x,y,λ)=(x,y)+λ(x+2y-4)=x2+y2+xy+λ(x+2y-4),