【正确答案】:
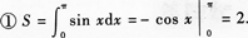
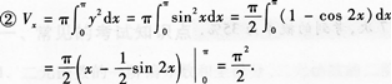
【题目解析】:对于①,曲线$y=\sin x$在区间$(0,\pi)$上与$x$轴围成的图形面积,根据定积分的几何意义,等于$\int_{0}^{\pi}\sin xdx$,计算可得$-\cos x\vert_{0}^{\pi}=(-\cos\pi)-(-\cos0)=2$,所以面积$S=2$。 对于②,该平面图形绕$x$轴旋转一周所得旋转体的体积,利用旋转体体积公式$V=\pi\int_{a}^{b}[f(x)]^{2}dx$,可得$V_x=\pi\int_{0}^{\pi}\sin^{2}xdx$,将$\sin^{2}x=\frac{1-\cos2x}{2}$代入计算可得具体结果。
