【正确答案】:
①如图1—3-6所示,由已知条件可得
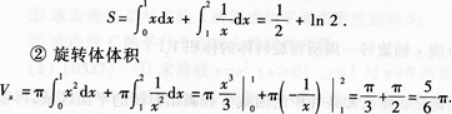
【题目解析】:[填空题]①求由曲线$y=x$,$y=1 / x$,$x=2$与$y=0$所围成的平面图形的面积$S$; 联立$y=x$与$y=1 / x$可得$x=1$或$x=-1$(舍去)则可得分界点为$x=1$。 因此,所求图形的面积可以分解为两个部分:曲线$y=x$,$y=1 / x$与$x=1$所围成的图形面积$S_1$;直线$y=0$,$x=1$与$x=2$所围成的图形面积$S_2$; 则有$S=S_1+S_2$。其中,$S_1$可以通过对曲线$y=x$从$0$到$1$进行积分得到,$S_2$可以通过对曲线$y=1 / x$从$1$到$2$进行积分得到。 即: $S=\int_0^1x\mathrm{d}x+\int_1^21 / x\mathrm{d}x$ 解得: $S=(\frac{1}{2}x^2)|_0^1+(\ln x)|_1^2$ $S=\frac{1}{2}+(\ln2-\ln1)$ $S=\frac{1}{2}+\ln2$ ②求①中的平面图形绕$x$轴旋转一周所得旋转体的体积$V$。 联立$y=x$与$y=1 / x$可得$x=1$或$x=-1$(舍去)则可得分界点为$x=1$。 因此,所求图形绕$x$轴旋转一周所得旋转体的体积可以分解为两个部分:曲线$y=x$,$y=1 / x$与$x=1$所围成的图形绕$x$轴旋转一周所得旋转体的体积$V_1$;直线$y=0$,$x=1$与$x=2$所围成的图形绕$x$轴旋转一周所得旋转体的体积$V_2$。 则有$V=V_1+V_2$。其中,$V_1$可以通过对曲线$y=x$从$0$到$1$绕$x$轴旋转一周所得旋转体的体积进行积分得到,$V_2$可以通过对曲线$y=1 / x$从$1$到$2$绕$x$轴旋转一周所得旋转体的体积进行积分得到。 即: $V=\int_0^1πx^2\mathrm{d}x+\int_1^2-π(1 / x)^2\mathrm{d}x$ 解得: $V=(\frac{1}{3}πx^3)|_0^1-π(\frac{1}{x})|_1^2$ $V=\frac{1}{3}π-π(\frac{1}{2}-1)$ $V=\frac{1}{3}π-π(\frac{1}{2}-1)$ $V=\frac{1}{3}π-\frac{1}{2}π$ $V=-\frac{π}{6}$
