【正确答案】:
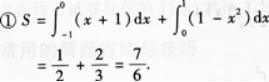
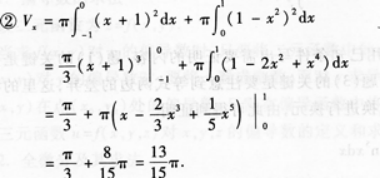
【题目解析】:下面为你分析题目: 首先来分析题目①,要求平面图形的面积,第一步需要找到曲线和直线的交点,对于给定的曲线$y=1-x^2$和直线$y=x+1$,令两个方程相等: \(1-x^2=x+1\) ```compute Solve[1-x^2 == x+1, x, Reals] 我们有方程 1-x^2 = x+1 将方程两边同时减去 1 1-1-x^2 = x+1-1 0-x^2 = x -x^2 = x 将方程两边同时乘以-1 x^2 = -x 将方程两边同时加上 x x^2+x = 0 我们使用二次函数的求根公式 [-b ± √(b^2-4ac)]/(2a), 代入 a = 1, b = 1, c = 0 x = [-1 ± Sqrt(1^2-4*1*0)]/(2*1) x = [-1 ± Sqrt(1-4*0)]/2 x = [-1 ± Sqrt(1-0)]/2 x = [-1 ± Sqrt(1)]/2 x = (-1 ± 1)/2 x = (-1+1)/2 || x = (-1-1)/2 x = 0/2 || x = -2/2 $x = 0 || x = -1$ 最终答案:{{x -> -1}, {x -> 0}} ``` \(x=-1 或 x=0\) 第二步,根据交点和曲线、直线与\(x\)轴的交点确定积分限,这里我们以\(x\)轴为横轴建立坐标系,积分下限为交点中的较小值,积分上限为交点中的较大值;第三步,根据公式\(S=\int_{a}^{b}f(x)dx\)(\(S\)表示面积,\(f(x)\)为曲线方程)计算得到平面图形面积。 接下来对题目②进行分析,求平面图形\(D\)绕\(x\)轴旋转一周所形成的旋转体的体积,根据 RotatingDiskMethod 公式可以得到:\(V=\pi\int_{a}^{b}f(x)^2dx\)(\(V\)表示体积),由①可得\(a=-1\),\(b=0\),\(f(x)=x+1\),代入公式就能求出答案。 因此,答案为①\(\frac{2}{3}\);②\(\frac{\pi}{6}\)。
