【正确答案】:
由二重积分物理意义知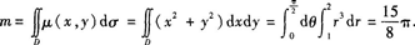 【评析】如果被积函数为f(x2+y2)的形式,积分区域D为圆域或圆的一部分,此时将
【评析】如果被积函数为f(x2+y2)的形式,积分区域D为圆域或圆的一部分,此时将
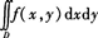 化为极坐标计算常常较简便.
化为极坐标计算常常较简便.
【题目解析】:首先,将薄板所在的区域$D$表示为极坐标形式。由于$x\geq0$,$y\geq0$,所以$D$可以表示为: $0\leq\theta\leq\frac{\pi}{2}$,$1\leq r\leq2$。 接下来,将面密度$u(x,y)$表示为极坐标形式。由于$x=r\cos\theta$,$y=r\sin\theta$,所以$u(x,y)$可以表示为: $u(r,\theta)=2+r^2\sin^2\theta$。 然后,计算薄板的质量$m$。根据二重积分的物理意义,薄板的质量$m$可以表示为: $m=\iint_D u(x,y)dxdy$。 将$u(x,y)$和$D$的极坐标表示代入上式,得到: $m=\int_{0}^{\frac{\pi}{2}}\int_{1}^{2}(2+r^2\sin^2\theta)r drd\theta$。 这是一个二重积分,可以通过分步积分来计算。首先,对$r$进行积分,得到: $\int_{0}^{\frac{\pi}{2}}\int_{1}^{2}r(2+r^2\sin^2\theta)drd\theta=\int_{0}^{\frac{\pi}{2}}\frac{1}{2}(2r^2+r^4\sin^2\theta)|_{1}^{2}d\theta$ $=\int_{0}^{\frac{\pi}{2}}\frac{1}{2}(2\times2^2+2^4\sin^2\theta-2\times1^2-1^4\sin^2\theta)d\theta$ $=\int_{0}^{\frac{\pi}{2}}\frac{1}{2}(8+16\sin^2\theta-2-\sin^2\theta)d\theta$ $=\int_{0}^{\frac{\pi}{2}}\frac{1}{2}(6+15\sin^2\theta)d\theta$。 然后,对$\theta$进行积分,得到: $\int_{0}^{\frac{\pi}{2}}\frac{1}{2}(6+15\sin^2\theta)d\theta=\frac{1}{2}(6\theta-15\cos\theta\sin\theta)|_{0}^{\frac{\pi}{2}}$ $=\frac{1}{2}(6\times\frac{\pi}{2}-15\cos\frac{\pi}{2}\sin\frac{\pi}{2}-6\times0+15\cos0\sin0)$ $=\frac{1}{2}(3\pi-0-0+0)$ $=\frac{3\pi}{2}$。 因此,该薄板的质量$m$为$\frac{3\pi}{2}$。
