【正确答案】:
已知平面的法线向量n1=(2,-1,3),所求平面与已知平面平行,因此可取所求平面的法线向量n=n1=(2,-1,3),又平面过原点(0,0,0),由平面的点法式方程可知,所求平面方程为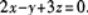
【题目解析】:根据题目所提供的信息,所求平面过原点且与平面\(2x-y+3z+5=0\)平行。由于平行平面具有相同的法线向量,所以可以先求出给定平面的法线向量。法线向量的分量就是平面方程中\(x,y,z\)的系数,所以给定平面的法线向量为\((2,-1,3)\)。 已知所求平面过原点,根据平面的点法式方程,可以直接写出所求平面的方程为: \(2x-y+3z=0\) 故答案为:\(2x-y+3z=0\)。
