【正确答案】：
由于已知平面的法线向量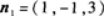
所求平面与已知平面平行，可取所求平面法线向量
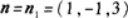又平面过点Mo(1，-1，0)，由平面的点法式方程可知，所求平面为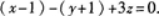
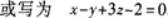【评析】上述两种形式都正确．前者为平面的点法式方程；后者为平面的一般式方程．
【题目解析】：首先，根据点法式平面方程的定义，点法式平面方程的一般形式为$A(x-x_0)+B(y-y_0)+C(z-z_0)=0$，其中$(x_0,y_0,z_0)$是平面上的一个点。已知平面的法线向量为$(1,-1,3)$，与所求平面平行，则可取所求平面的法线向量为$(1,-1,3)$。接下来，将点$M_0(1,-1,0)$和该法线向量代入上述平面方程中，得到所求平面为$(x-1)-(y+1)+3z=0$。综上，答案为$x-y+3z-2=0$。