【正确答案】：
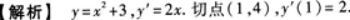故切线l的方程为y=2x+2．
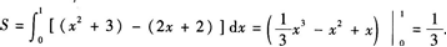
【题目解析】：首先对曲线\(y=x^2+3\)求导，可得\(y^\prime=2x\)。 将\(x=1\)代入导数中，可得切线的斜率为：\(2\times1=2\)。 已知切线过点\((1,4)\)，根据点斜式方程可得切线方程为：\(y-4=2(x-1)\)，整理得：\(y=2x+2\)。 接下来计算平面图形的面积。 曲线与\(y\)轴的交点为\((0,3)\)，切线与\(y\)轴的交点为\((0,2)\)。 则所求平面图形的面积为： \[ \begin{align*} S&=\int_0^1(x^2+3-2x-2)dx\\ &=\int_0^1(x^2-2x+1)dx\\ &=\frac{1}{3}x^3-x^2+x\Big|_0^1\\ &=\frac{1}{3}-1+1-\left(0-0+0\right)\\ &=\frac{1}{3} \end{align*} \] 综上所述，平面图形的面积\(S=\frac{1}{3}\)。