【正确答案】:
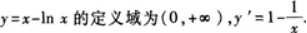
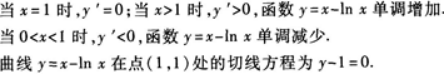 【评析】求函数f(x)的单调区间,应先判定函数的定义域.求出函数的驻点,即y′=0的点;求出y的不可导的点,再找出y′>0时x的取值范围,这个范围可能是一个区间,也可能为几个区间.
【评析】求函数f(x)的单调区间,应先判定函数的定义域.求出函数的驻点,即y′=0的点;求出y的不可导的点,再找出y′>0时x的取值范围,这个范围可能是一个区间,也可能为几个区间.【题目解析】:函数$y=x-\ln x$的定义域为$(0,+\infty)$。对$y=x-\ln x$求导得到: \[ y'=1-\frac{1}{x} \] 令$y'=0$,解得$x=1$。当$0
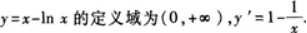
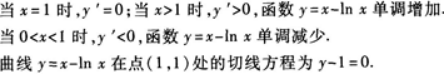 【评析】求函数f(x)的单调区间,应先判定函数的定义域.求出函数的驻点,即y′=0的点;求出y的不可导的点,再找出y′>0时x的取值范围,这个范围可能是一个区间,也可能为几个区间.
【评析】求函数f(x)的单调区间,应先判定函数的定义域.求出函数的驻点,即y′=0的点;求出y的不可导的点,再找出y′>0时x的取值范围,这个范围可能是一个区间,也可能为几个区间.