【正确答案】:
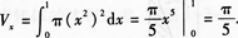
【题目解析】:曲边梯形绕\(x\)轴旋转一周所得旋转体体积为: \[ \begin{align*}V&=\pi\int_0^1y^2dx\\&=\pi\int_0^1x^2\times(x^2)dx\\&=\pi\int_0^1x^4dx\\&=\pi\times\frac{1}{5}x^5\vert_0^1\\&=\pi\times(\frac{1}{5}\times1^5-\frac{1}{5}\times0^5)\\&=\frac{\pi}{5}\end{align*} \] 所以正确答案为\(\frac{\pi}{5}\)。
