【正确答案】:

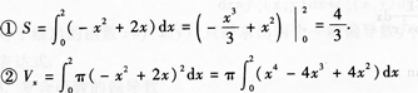
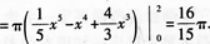
【题目解析】:①要求曲线$y=f(x)=-x^2+2x$与$x$轴所围成的平面图形面积。令$y=0$,即$-x^2+2x=0$,$x(-x+2)=0$,解得$x=0$或$x=2$。则曲线与$x$轴交点为$(0,0)$和$(2,0)$。 $S=\int_{0}^{2}(-x^2+2x)dx=(-\frac{1}{3}x^3+x^2)\mid_{0}^{2}=(-\frac{8}{3}+4)= \frac{4}{3}$。 ②该平面图形绕$x$轴旋转一周所得旋转体体积,使用圆柱体积公式的定积分形式。 $V_x=\pi\int_{0}^{2}(-x^2+2x)^2dx=\pi\int_{0}^{2}(x^4-4x^3+4x^2)dx=\pi(\frac{1}{5}x^5-x^4+\frac{4}{3}x^3)\mid_{0}^{2}=\pi(\frac{32}{5}-16+\frac{32}{3})=\frac{16\pi}{15}$。
