【正确答案】:
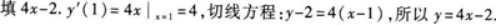
【题目解析】:首先,我们需要求出函数$y = 2x^2$的导数。利用导数的定义或基本导数公式,我们得到: $y' = \frac{d}{dx}(2x^2) = 4x$ 接下来,我们需要求出在点$(1, 2)$处的导数值,即切线的斜率。将$x = 1$代入导数表达式中,得到: $y'|_{x=1} = 4 \times 1 = 4$ 所以,在点$(1, 2)$处的切线斜率为$4$。 最后,利用点斜式方程$y - y_1 = m(x - x_1)$,其中$(x_1, y_1) = (1, 2)$,$m = 4$,我们可以得到切线方程为: $y - 2 = 4(x - 1)$ 化简后得到: $y = 4x - 2$ 这就是曲线$y = 2x^2$在点$(1, 2)$处的切线方程。
