【正确答案】:
①'(x)=3ax2+2bx+1.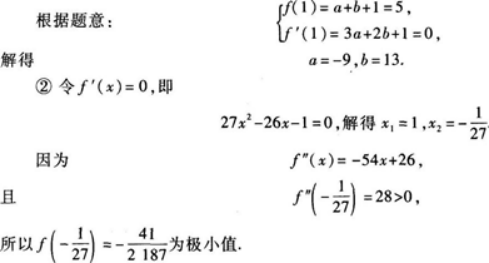
【题目解析】:①由题可知,\(f^\prime(1)=0\),且\(f(1)=5\) ,即: \(\begin{cases} 3a+2b+1=0 \\ a+b+1=5 \end{cases}\) 解得:\(\begin{cases} a=-12 \\ b=16 \end{cases}\) 所以,常数\(a\)和\(b\)的值分别为:\(a=-12\),\(b=16\)。 ②由①可得:\(f(x)=-12x^3+16x^2+x\) \(f^\prime(x)=-36x^2+32x+1\) 令\(f^\prime(x)=0\),解得:\(x_1=1\),\(x_2=\frac{1}{9}\) 所以,\(f(x)\)在\((-\infty,\frac{1}{9})\)和\((1,+\infty)\)上单调递减,在\((\frac{1}{9},1)\)上单调递增。 所以,\(f(x)\)在\(x=\frac{1}{9}\)处取得极小值,极小值为: \(f(\frac{1}{9})=-12\times(\frac{1}{9})^3+16\times(\frac{1}{9})^2+\frac{1}{9}=\frac{4}{243}\) 所以,函数\(f(x)\)的极小值为\(\frac{4}{243}\)。 因此,答案为:①\(a=-12\),\(b=16\);②\(\frac{4}{243}\)。
