【正确答案】：
由二阶线性常系数微分方程解的结构可知所给方程的通解为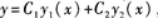
其中C1，C2为任意常数．
【题目解析】：二阶常系数线性微分方程 y″+py′+qy=0 的特征方程为$r^2+pr+q=0$。根据特征方程的根的情况，我们可以得到不同类型的通解。本题中，已知 y1(x)、y2(x)是该方程的两个线性无关的解，因此它们满足该方程。根据线性无关的定义，y1(x)和 y2(x)的比值不为常数。这意味着它们不是同一个解的倍数，而是两个独立的解。因此，我们可以使用通解的形式$y=C_1y_1(x)+C_2y_2(x)$，其中 C1、C2 为任意常数。因此，所给方程的通解为$\underline{y=C_1y_1(x)+C_2y_2(x)}$，其中 C1，C2 为任意常数。