【正确答案】：
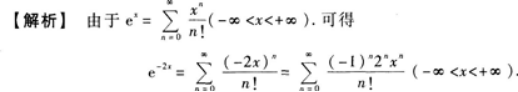【评析】将函数展开为幂级数，通常将函数与标准展开式中的函数对照．展开为幂级数之后一定要注明收敛域．【题目解析】：根据已知的泰勒展开式 \(e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+...\) 可得： \(e^{-2x}=\sum_{n=0}^{\infty}\frac{(-2x)^n}{n!}=\sum_{n=0}^{\infty}\frac{(-2)^nx^n}{n!}=1-2x+\frac{(-2)^2x^2}{2!}+\frac{(-2)^3x^3}{3!}+...\) 因此，函数\(f(x)=e^{-2x}\)展开为 x 的幂级数为\(\sum_{n=0}^{\infty}\frac{(-2)^nx^n}{n!}\)。由于幂级数在其收敛域内是绝对收敛的，而\(\sum_{n=0}^{\infty}\frac{(-2)^nx^n}{n!}\)的收敛半径是\(\infty\)，所以该幂级数的收敛域是\((-\infty,\infty)\)。