【正确答案】:
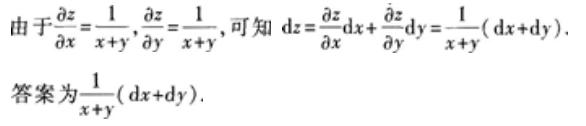
【题目解析】:首先,根据链式法则,对函数$z=\ln(x+y)$关于$x$求偏导数,得到: $\frac{\partial z}{\partial x}=\frac{1}{x+y}$ 然后,对函数$z=\ln(x+y)$关于$y$求偏导数,得到: $\frac{\partial z}{\partial y}=\frac{1}{x+y}$ 最后,根据全微分的定义,$dz=\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}dy$,将上面求得的偏导数代入,得到: $dz=\frac{1}{x+y}dx+\frac{1}{x+y}dy=\frac{1}{x+y}(dx+dy)$ 因此,全微分$dz=\frac{1}{x+y}(dx+dy)$。
