计算题
假设有两个生产同质产品的寡头垄断企业的成本函数分别为: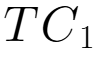 =0.1
=0.1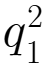 +20
+20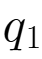 +100000
+100000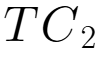 =0.4
=0.4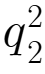 +32
+32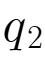 +200000其市场需求函数为:Q=4000-10P。请根据古诺模型,求市场均衡时的价格、两个企业各自的产量以及各自的利润。
+200000其市场需求函数为:Q=4000-10P。请根据古诺模型,求市场均衡时的价格、两个企业各自的产量以及各自的利润。
【正确答案】:
由Q=4000-10P,则P=400-0.1Q,其中Q=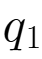 +
+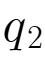 可得到
可得到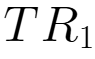 =P×
=P×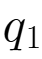 =(400-0.1
=(400-0.1 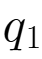 -0.1
-0.1 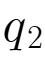 )×
)×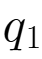 =400
=400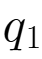 -0.1
-0.1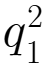 -0.1
-0.1 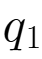
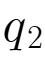
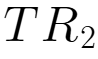 =P×
=P×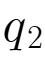 =(400-0.1
=(400-0.1 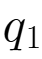 -0.1
-0.1 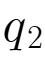 )×
)×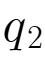 =400
=400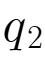 -0.1
-0.1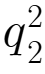 -0.1
-0.1 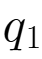
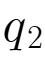 由此可得到
由此可得到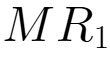 =400-0.2
=400-0.2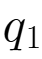 -0.1
-0.1 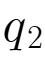
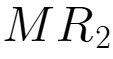 =400-0.2
=400-0.2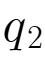 -0.1
-0.1 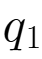 由于企业实现利润最大化,因此会有
由于企业实现利润最大化,因此会有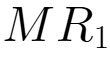 =
=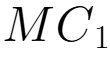 ,
,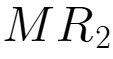 =
=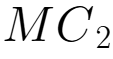 ,由此可得
,由此可得
400-0.2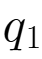 -0.1
-0.1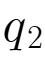 =0.2
=0.2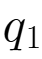 +20,
+20,
400-0.2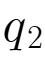 -0.1
-0.1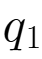 =0.2
=0.2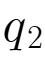 +32,
+32,
可得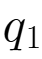 =950-0.25
=950-0.25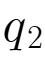 (企业1对于企业2的最优反应函数),
(企业1对于企业2的最优反应函数),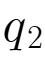 =368-0.1
=368-0.1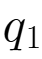 (企业2对于企业1的最优反应函数),
(企业2对于企业1的最优反应函数),
联立两个最优反应函数,可求解得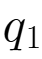 =880,
=880,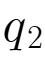 =280
=280
则Q=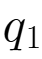 +
+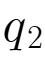 =1160,均衡价格P=400-0.1×1160=284,
=1160,均衡价格P=400-0.1×1160=284,
两个企业此时的利润分别为: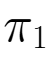 =
=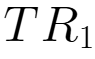 -
-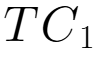 =54880,
=54880,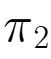 =
=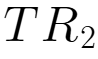 -
-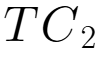 =
=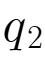 =19200
=19200
