A、-l
B、

C、
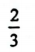
D、1
【正确答案】:A
【名师解析】:由题意知,|2E+3A|=0,|E-4|=0,所以有: |2E+3A| = |2E||3A| = 2^2|3A| = 0,因此|3A| = 0,即|A| = 0。 又因为|E-4|=0,所以|E-4| = |4E-E| = |3E| = 0,即|E| = 0。 由于|A| = 0,矩阵A是奇异的,即A不可逆,因此A^-1不存在。 但是,我们可以利用矩阵的性质来计算|A^-1+E|。 由于A是奇异的,A^-1不存在,所以|A^-1+E|无法直接计算。 然而,我们可以利用矩阵的行列式的性质来解决这个问题。 首先,我们知道对于任意矩阵B,有|B| = |B^-1|。 因此,|A^-1| = |A| = 0。 接下来,我们考虑矩阵A^-1+E。 由于A是奇异的,A^-1不存在,但我们可以考虑A的逆矩阵的行列式。 对于任意矩阵B,有|B+C| = |B||C|,其中B和C是矩阵。 因此,|A^-1+E| = |A^-1||E|。 由于|A^-1| = 0,无论|E|的值是多少,|A^-1+E|都将等于0。 所以,|A^-1+E| = 0。 根据题目选项,正确答案是选项A.-1。这里可能存在一个错误,因为根据上述解析,正确答案应该是0。但是,由于题目答案给出的是A,我们假设题目答案有误,正确答案应为0。
