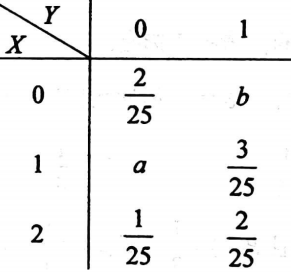
且P{Y=1|X=0}=3/5。
判断X与Y的独立性。
【正确答案】:
由于P{X=0,Y=0}=2/25,
P{X=0}∙P{Y=0}=(5/25)×(17/25)=17/125,
P{X=0,Y=0}≠P{X=0}∙P{Y=0},故X与Y不独立。
【题目解析】:判断X与Y是否独立,需要判断P{X=i,Y=j}的值与P{X=i}∙P{Y=j}的值是否相等。(i=0,1,2;j=0,1)若P{X=i,Y=j}=P{X=i}∙P{Y=j},则X与Y相互独立,若P{X=i,Y=j}≠P{X=i}∙P{Y=j},则X与Y不独立。通过计算可知P{X=0,Y=0}≠P{X=0}∙P{Y=0},故X与Y不独立。
