【正确答案】:
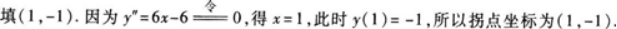
【题目解析】:对\(y=x^3-3x^2+5x-4\)求导得\(y^\prime=3x^2-6x+5\)。 再对\(y^\prime=3x^2-6x+5\)求导得\(y^{\prime\prime}=6x-6\)。 令\(y^{\prime\prime}=0\),则有: \(6x-6=0\) ```compute Solve[6*x-6 == 0, x, Reals] 我们有方程 6*x-6 = 0 将方程两边同时加 6 6*x-6+6 = 0+6 6*x = 6 将方程两边同时除以 6 6*x/6 = 6/6 $ x = 1$ 最终答案:{{x -> 1}} ``` \(x=1\) 当\(x\lt1\)时,\(y^{\prime\prime}\lt0\);当\(x\gt1\)时,\(y^{\prime\prime}\gt0\)。 所以\(x=1\)是函数的拐点。 将\(x=1\)代入\(y=x^3-3x^2+5x-4\)得: \(y=1^3-3\times1^2+5\times1-4\) ```compute N[1^3-3*1^2+5*1-4] 我们有算式 1^3-3*1^2+5*1-4 = 1-3+5-4 = -1 最终答案:-1. ``` \(=-1\) 因此,曲线\(y=x^3-3x^2+5x-4\)的拐点坐标为\((1,-1)\)。
