【正确答案】:
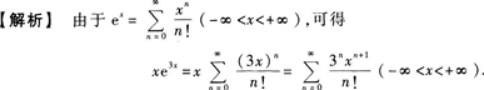
【题目解析】:首先,对$f(x)=xe^{3x}$进行展开。 根据幂级数的展开公式$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots+\frac{x^n}{n!}+\cdots$,将$e^{3x}$展开: $e^{3x}=1+3x+\frac{(3x)^2}{2!}+\frac{(3x)^3}{3!}+\cdots+\frac{(3x)^n}{n!}+\cdots$ 将其乘以$x$,得到$f(x)=xe^{3x}$的展开式: $f(x)=x+3x^2+\frac{9x^3}{2}+\frac{27x^4}{6}+\cdots+\frac{3^n x^{n+1}}{n!}+\cdots$ 接下来,要求出该幂级数的收敛区间。 根据幂级数的收敛性质,当幂级数的通项系数趋于零时,幂级数收敛。 对于$f(x)$的幂级数,通项系数为$a_n=\frac{3^n}{n!}$。 当$x$固定时,$n$趋近于无穷时,$\frac{3^n}{n!}$趋近于零。 因此,幂级数$f(x)$对任意$x$都收敛。 综上,答案为$f(x)=x+3x^2+\frac{9x^3}{2}+\frac{27x^4}{6}+\cdots+\frac{3^n x^{n+1}}{n!}+\cdots$,收敛区间为$(-\infty,+\infty)$。
