【正确答案】:
将2y+sin(x+y)=0两边对x求导,得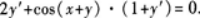
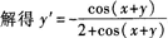
【题目解析】:根据隐函数求导法则,设函数$F(x,y)$在点$(x_0,y_0)$的某邻域内具有连续偏导数,且$F(x_0,y_0)=0$,$F_y(x_0,y_0)\neq0$,则方程$F(x,y)=0$在点$(x_0,y_0)$的某邻域内可唯一确定一个函数$y=f(x)$,满足$y_0=f(x_0)$,并有: $\frac{dy}{dx}=-\frac{F_x(x,y)}{F_y(x,y)}$ 对于本题,设$F(x,y)=2y+sin(x+y)$,则: $F_x(x,y)=cos(x+y)$ $F_y(x,y)=2+cos(x+y)$ 将$F_x(x,y)$和$F_y(x,y)$代入隐函数求导法则中,得到: $\frac{dy}{dx}=-\frac{F_x(x,y)}{F_y(x,y)}=-\frac{cos(x+y)}{2+cos(x+y)}$ 因此,$y^\prime=-\frac{cos(x+y)}{2+cos(x+y)}$。
