【正确答案】:
y=xlnx的定义域为x>0.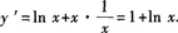

【题目解析】:首先,我们来分析题目。 这道题主要考察了函数的单调性以及求导的知识点。 接下来我们详细分析其推理过程: 根据题目所给,需要求出函数$Y=x\ln x$的单调增加区间。 因为函数的单调性可以通过其导数的正负情况来判断,所以我们先对函数$Y=x\ln x$进行求导: 根据求导公式:若$f(X)=X^n$,则$f^\prime(X)=nX^{n-1}$,以及$\ln^\prime x=\frac{1}{x}$。 所以对$Y=x\ln x$求导得:$Y^\prime=\ln x+1$ 然后,我们需要找到$Y^\prime$大于0 的区间,因为$Y^\prime$大于0 时函数单调递增。 即:$\ln x+1\gt0$ 移项得:$\ln x\gt-1$ 因为对数函数$ln x$是单调递增的,所以当$ln x\gt-1$时,$x\gt e^{-1}$。 又因为函数$Y=x\ln x$的定义域为$x\gt0$。 综上可得,函数$Y=x\ln x$的单调增加区间是$(e^{-1},+\infty)$。
